Programming with Effect Handlers in Links (1)
Plotkin and Power's algebraic effects [1] combined with Plotkin and Pretnar's handlers [2] provide an approach to model and control side-effecting computations. In my master's project at the University of Edinburgh I implemented effect handlers in the functional programming language Links [3]. Through a series of posts I will demonstrate how to program with effect handlers in Links. In this first part, we will mainly focus on building intuition for programming with handlers by using a coin toss as a running example. Our coin toss model will encompass effects such as nondeterminism and exceptions. Through handlers we will give different interpretations of a coin toss.
Installing Links with effect handlers
Links is a research language mainly oriented towards web-programming. It is being developed at the University of Edinburgh [4].
The examples in this blog post (and future ones) are meant to be evaluated in Links as you go. Thus, you possibly want to have a working installation of Links with effect handlers. To obtain the source you have to clone the effect-handlers branch from the Links git repository, e.g.
$ git clone -b effect-handlers git@github.com:links-lang/links.gitIf successful, you should now have a directoy called "links". Inside it you will find instructions (see INSTALL) on how to build and install Links. Note, we will not use any of the web-related features in Links, hence it is not necessary to configure Links for web-programming. After building Links you should be able to type rlwrap ./links on the commandline which should take you into the Links toplevel:
_ _ __ _ _ __ ___
/ | | | \ | | |/ / / ._\
| | | | , \| | / \ \
| |___| | |\ \ | |\ \ _\ \
|_____|_|_| \__|_| \_|____/
Welcome to Links with effect handlers
links> Type @directives; for further help.
Nondeterministic choice
An algebraic effect is a collection of abstract operations [1], e.g. \( Choice = \{Choose:\texttt{Bool} \}\) defines an algebraic effect \(Choice\) that has one abstract operation \(Choose\). The signature of \(Choose\) tells us that it returns a value of type \(\texttt{Bool}\). In Links, we may use the operation to implement a binary choice as follows:
sig choose : (a,a) {Choose:Bool|e}~> Bool
fun choose(x,y) {
if (do Choose) {x} else {y}
}Here, we defined a function choose which takes two arguments of type a, and returns one of them. In order to decide which argument to return it invokes an operation Choose by using the do-primitive. Notice that, operation names start with an uppercase letter, whilst function names start with a lowercase letter. The do-primitive is an artefact from the backend which leaked into the frontend syntax due to lack of better alternatives. It is subject to change in the future.
The signature for choose conveys that the function returns a value of type a, however, before returning it may invoke Choose. In Links function arrows are annotated with an effect signature which conveys which operations the function might invoke during evaluation. Observe the resemblance between the effect signature and the definition of \(Choice\). Albeit, the signature for choose has an extra variable e. Links employ row typing for effect signature (records and variants too!), hence e is a row variable which can be instantiated to additional effects. Intuitively, this means that the function choose may be used in conjunction with other effectful functions. In a later post, we will discuss row typing in more detail.
Since Links employs structural typing we do not need to give a name to our effects, in fact, it is not possible to give names to effects in Links at the time of writing. Incidentally, the notions of effect and abstract operation coincide in Links. Thus, I will use terminology effects and (abstract) operations interchangably.
Coin tossing
So far, we have defined one effect Choose. We can use this to model a nondeterministic computation such as a coin toss. Consider the following computation toss:
typename Toss = [|Heads|Tails|];
sig toss : () {Choose:Bool|_}~> Toss
fun toss() { choose(Heads,Tails) }First, we define a sum type Toss, which models the two possible outcomes of a single coin toss. Next, we define a computation toss that either returns Heads or Tails. The outcome depends on the return value of choose. Note, that we have hidden the name of the row variable in the effect signature using _, because it only occurs once. On the Links toplevel, we may try to evaluate the computation, e.g.
links> toss();
*** Error: Evalir.Eval.EvaluationError("Unhandled operation: Choose")Choose. It is really saying that, it does not know how to interpret the operation Choose. In fact, the computation toss is an abstract computation. An abstract computation is composed from one or more abstract operations [3]. Furthermore, an abstract computation is syntactical, it has no particular semantics. We can visualise an abstract computation as a computation tree. For example, Figure 1 depicts the computation tree of toss.

toss.
The computation tree in Figure 1 only has three nodes. In general, we have two types of nodes: "operation/effect"-nodes and "data"-nodes. The operation nodes (coloured blue in Figure 1) correspond to abstract operations in the computation. Data nodes correspond to concrete return values of the computation, thus a data node will always be a leaf in the computation tree.
Handlers assign semantics to abstract operations in some computation. In Links, we can define a simple handler positive which interprets Choose as being true:
typename Comp(e::Row,a) = () ~e~> a;
sig positive : (Comp({Choose:Bool}, a)) {}~> a
handler positive(m) {
case Choose(k) -> k(true)
case Return(x) -> x
}The type Comp(e,a) is a type alias for a nullary function with effect signature e and return type a. Essentially, the positive handler pattern matches on operations that might occur inside the computation m. The signature for positive conveys that it accepts a computation, that might invoke the Choose operation and return some value of type a. Furthermore, the effect signature on the handler is empty, meaning that no further effects will occur. The handler exposes a parameter k in the case for Choose. The k is a continuation captured at the point in the computation m when the operation Choose was invoked. Thus, invoking k with true basically "replaces" the occurrence of Choose in m with the value true. Moreover, Return is an implicit effect that is invoked when the computation m finishes. The parameter x is the concrete return value of the computation; a handler may transform the value of a computaton, however, in this case we simply apply the identity transformation. Handlers have pleasing visual interpretation. For example, the positive-handler on toss traverses the computation tree of toss, when it visits a Choose-node it takes the true-branch (left-branch on Figure 1). When it hits a leaf node it simply returns the value.
Now, we can evaluate the computation toss using the handler positive in the toplevel:
links> positive(toss);
Heads : TossWhenever toss is evaluated using positive, we get Heads. We can consider another interpretation of Choose, e.g.
sig allResults : (Comp({Choose:Bool}, a)) {}~> [a]
handler allResults(m) {
case Choose(k) -> k(true) ++ k(false)
case Return(x) -> [x]
}The signature for this handler looks similar to the signature of positive. However, unlike the positive-handler, the allResults-handler returns a list of elements of type a. Basically, this handler enumerates the sample space by first visiting the left-branch (k(true)) in the computation tree. Afterwards, it visits the right branch (k(false)). The results of the two continuation invocations are concatenated using the list concatenation operator ++. The Return-case lifts a leaf node into a singleton list. This interpretation enumerates the possible outcomes of a single coin toss:
links> allResults(toss);
[Heads, Tails] : [Toss]Notice, that we have only changed the interpretation of Choose; we have not changed the computation toss, it remains the same.
Drunk coin tossing
Let us extend the coin tossing example by modelling a drunk coin toss. A drunkard may fail to catch the coin after the toss. We will introduce another effect \(\{Failure : \texttt{Void}\} \) to capture the possibility of failure. The type \(Void\) is the empty type which implies \(Failure\) never returns a value. The drunk coin tossing example is based on a similar example from Kammar et al. [5].
Like before with Choose, we abstract over Failure:
typename Void = [||];
sig fail : Comp({Failure:Void|_},a)
fun fail() { switch (do Failure) {} }The function fail invokes the operation Failure, but it will never return anything (the type system will enforce every handler for Failure to comply with this requirement).
The following computation models a drunk coin toss:
sig drunkToss : Comp({Choose:Bool,Failure:Void|_}, Toss)
fun drunkToss() {
if (choose(true,false)) {
toss()
} else {
fail()
}
}true and false, if we get true then we evaluate our toss-computation from before, otherwise we fail. Figure 2 depicts the computation tree for drunkToss.
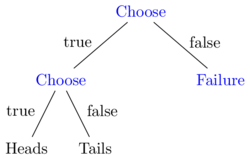
drunkToss.
The Choose-operation is potentially invoked twice; first to decide whether to toss or fail. If true is chosen, then the toss-computation invokes Choose again to pick either Heads or Tails. In the event of failure the computation drunkToss will not return a value. Essentially, invoking Failure is similar to signalling an exception.
If we try to evaluate drunkToss under allResults (or positive for that matter) the Links interpreter sends us its regards:
links> allResults(drunkToss);
Type error: The function
`allResults'
has type
`(() {Choose:Bool}~> a) {}~> [a]'
while the arguments passed to it have types
`Comp ({ Choose:Bool,Failure:Void|a },Toss)'
and the currently allowed effects are
`Choose:Bool,Failure:Void,wild|_'.
In expression: allResults(drunkToss).The error message is basically telling us that allResults is not interpreting (handling) the operation Failure. Now, we could extend allResults with a case to cover Failure. Alternatively, we can shift the interpretation of Failure onto another handler.
Open handlers
The handlers allResults and positive are said to be closed handlers. Intuitively, a closed handler imposes an upper bound on which effects may occur in a given computation. Moreover, all effects in the computation will be handled by the closed handler. In contrast open handlers handle a particular subset of the effects that may occur in a computation, and leaves the interpretation of remainder to other handlers. An open handler takes a computation \(Comp(E,a)\) and produces another computation \(Comp(E',a')\). Thus, we may construct an interpretation of a given computation through composition of several open handlers. Therefore we may define small, specialised handlers that each give an interpretation to, say, a single effect. Then, we may compose a variety of handlers to obtain different interpretations of computations.
Let us define an (open) exception handler for Failure:
typename Maybe(a) = [|Just:(a)|Nothing|];
sig maybeResult : (Comp({Failure:Void|e}, a) -> Comp({Failure{_}|e}, Maybe(a))
open handler maybeResult(m) {
case Failure(_) -> Nothing
case Return(x) -> Just(x)
}In the event of Failure, the handler returns Nothing, otherwise it returns Just the result. Notice that in the type signature for maybeResult the row variable e occurs in both effect signatures. The row variable e propogates information about which effects are present in the computation. The notation Failure{_} denotes that the operation may be present or absent in the computation. This is important for composition as this information enables us to compose maybeResult with another handler that may or may not handle Failure. Furthermore, it allows us to compose maybeResult with a closed handler like allResults. When applying allResults to maybeResult forces Failure to be absent from the composed computation as allResults only handles Choose. For example, we can ask the Links interpreter to infer the type signature of the composition:
links> fun(m) { allResults(maybeResult(m)) };
fun : (Comp ({Choose:Bool,Failure:Void},a)) {}~> [Maybe (a)]It infers the type of m to be a computation where Choose and Failure are present effects, however, as expected, the effect signature of the function itself is closed (signified by {}~>); the function produces a list of Maybe(a). We can use this composition to interpret drunkToss, e.g.
links> allResults(maybeResult(drunkToss));
[Just(Heads), Just(Tails), Nothing] : [Maybe(Toss)]The interpretation gives us all possible outcomes of a drunk coin toss.
Interpreting randomness
All our interpretations of toss and drunkToss have been deterministic so far. Let us introduce randomness as an effect. Like before, we abstract over the invocation of the effect itself:
sig rand : Comp({Rand:Float|_}, Float)
fun rand() {do Rand}The encoding of randomness as an effect lets us defer the decision of which random source to use. For example, we can choose to use Links' built-in random number generator:
sig handleRandom : (Comp({Rand:Float|e}, a)) -> Comp({Rand{_}|e}, a)
open handler handleRandom(m) {
case Rand(k) -> k(random())
case Return(x) -> x
}The handler simply invokes the continuation with a random float drawn from the interval \((0,1)\). If we interpret rand using handleRandom we ought to see some random floating point number such as
links> handleRandom(rand)();
0.887869906037 : Float
links> handleRandom(rand)();
0.272035879143 : Float
links> handleRandom(rand)();
0.688449095622 : FloatAlternatively, we could choose to use a deterministic source to interpret randomness which might sound like an odd thing to do, however, it can be useful for debugging/testing computations that use randomness.
Random coin tossing
We can give an alternative interpretation Choose using randomness:
sig randomResult : (Comp({Choose:Bool,Rand:Float|e}, a)) ->
Comp({Choose{_}, Rand:Float|e}, a)
open handler randomResult(m) {
case Choose(k) -> k(rand() < 0.5)
case Return(x) -> x
}The handler invokes rand to generate a random number; if the generated number is less than 0.5 then the continuation k is invoked with true, otherwise it is invoked with false. Notice that the operation Rand is present in both effect signatures, while Choose might be absent in the second signature. The presence of Rand in the second effect signature implies that it must be handled by another handler, e.g. handleRandom.
Composing handleRandom, randomResult and maybeResult together, we can give a nondeterministic interpretation of drunkToss:
links> handleRandom(randomResult(maybeResult(drunkToss)))();
Nothing : Maybe(Toss)
links> handleRandom(randomResult(maybeResult(drunkToss)))();
Just(Tails) : Maybe(Toss)
links> handleRandom(randomResult(maybeResult(drunkToss)))();
Just(Heads) : Maybe(Toss)These are the three possible outcomes. The maybeResult-handler short circuits the computation when the drunkard fails to catch the coin. Instead of circuiting the computation, we might want to start over. Let us define an exception handler persevere which restarts a computation in the event of Failure:
sig persevere : (Comp({Failure:Void|e}, a)) -> Comp({Failure{_}|e}, a)
open handler persevere(m) {
case Failure(_) -> persevere(m)()
case Return(x) -> x
}If the computation m fails, then the handler restarts the computation by applying itself recursively to m. When we use persevere to interpret drunkToss we will no longer witness a failure:
links> handleRandom(randomResult(persevere(drunkToss)))();
Heads : Toss
links> handleRandom(randomResult(persevere(drunkToss)))();
Tails : Toss
links> handleRandom(randomResult(persevere(drunkToss)))();
Tails : TossConclusion
We have seen three different effects: Choose, Failure and Rand which we have used to model a coin toss. The effects are entirely syntactical, they do not have a predefined semantics. Through handlers we can assign semantics to effects. The key observation is that handlers allow us to separate the syntax and semantics of effects. Consequently, we can control the interpretation of effects. Furthermore, the programming model is inherently modular as we can change the interpretation of a given computation by only changing the handler. In particular, we can extend an interpretation through composition of handlers as we saw with the drunkToss-computation. First, our interpretations were deterministic, later we added randomness to model a true coin toss. You may find the complete source code for the examples in this post.
The main goal of this post was to developed our intuition of handlers and effects. In the next post, we will introduce parameterised operations and handlers which enable us to interpret stateful computations. I will publish the next post in the coming week.
Addendum: Function arrows in Links
Links have multiple function arrows. In this post we have seen two different types of arrows: The squiggly arrow ~> and the straight arrow ->. The squiggly arrow is syntactic sugar for denoting an open effect row with a special, built-in effect known as "the wild effect". For instance, we could have written the type signature for choose as (a,a) {Choose:Bool,wild|_}-> a. The wild effect appears whenever a computation might have a side-effect such as printing to standard out or diverge. Most functions in the Links prelude allow the wild effect to occur. Therefore in order to write interesting programs, we need to include the wild effect. However, I often drop it and assume its presence implicitly. Thus I would pretty-print the signature of choose as \((a,a) \xrightarrow{\{Choose:\texttt{Bool}|\_\}} a \).
The straight arrow -> denotes an open empty effect signature.
References
[1] G. D. Plotkin and J. Power, “Adequacy for Algebraic Effects,” in Foundations of Software Science and Computation Structures, 4th International Conference, FOSSACS 2001 Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2001 Genova, Italy, April 2-6, 2001, Proceedings, 2001, vol. 2030, pp. 1–24.
[2] G. D. Plotkin and M. Pretnar, “Handling Algebraic Effects,” Logical Methods in Computer Science, vol. 9, no. 4, 2013.
[3] D. Hillerström, “Handlers for Algebraic Effects in Links,” Master’s thesis, School of Informatics, the University of Edinburgh; Supervised by Sam Lindley, Scotland, 2015.
[4] E. Cooper, S. Lindley, P. Wadler, and J. Yallop, “Links: Web Programming Without Tiers,” in Formal Methods for Components and Objects, 5th International Symposium, FMCO 2006, Amsterdam, The Netherlands, November 7-10, 2006, Revised Lectures, 2006, vol. 4709, pp. 266–296.
[5] O. Kammar, S. Lindley, and N. Oury, “Handlers in Action,” in Proceedings of the 18th ACM SIGPLAN International Conference on Functional Programming, 2013, pp. 145–158.